Details on B4

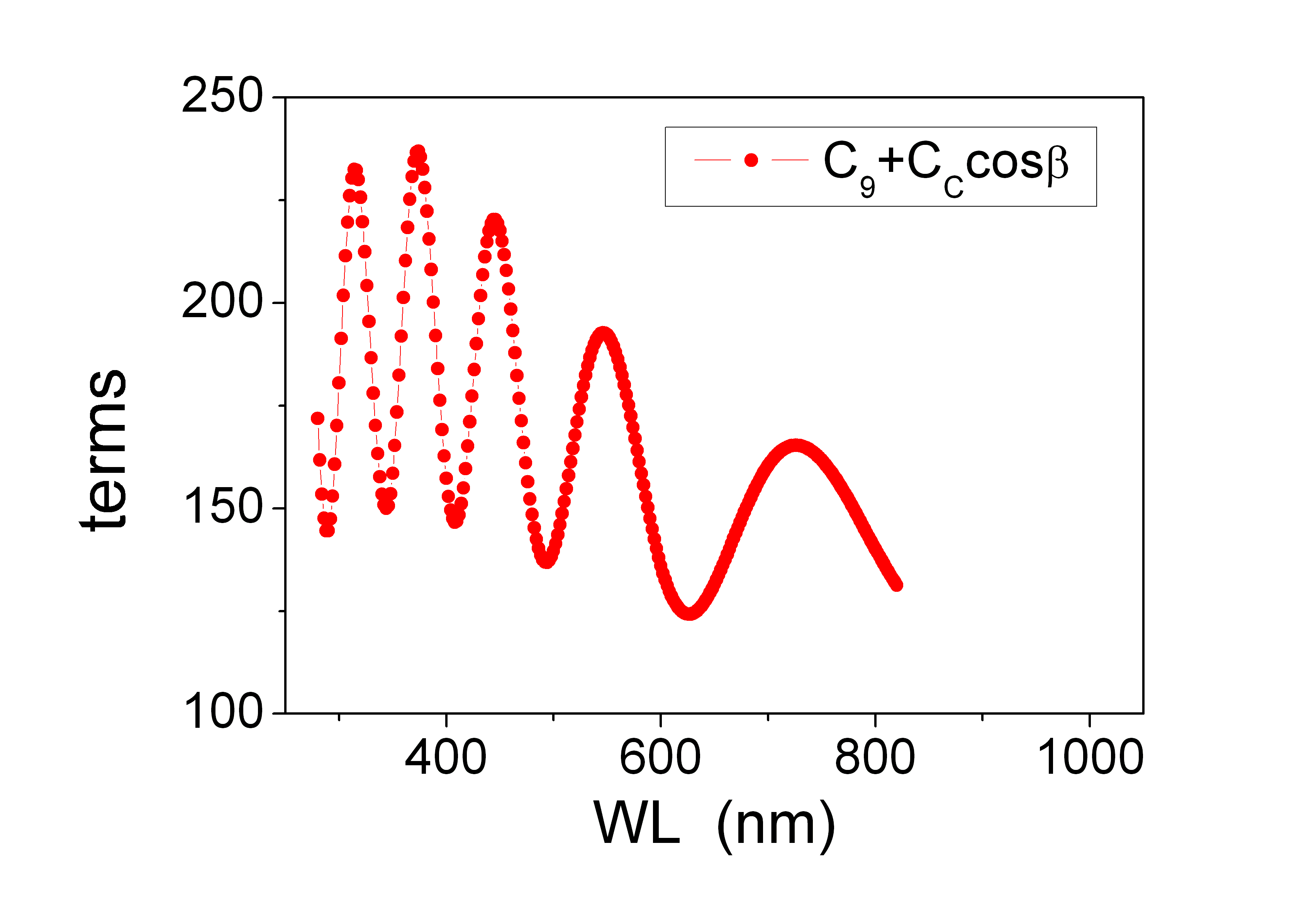
In the paper, the substitution of $B_4$ with its approximated value is given with little detail. The example below is given for an actual a-SiC:H sample. If we set:

$$G_1=2(C_A+C_B)-T_{NUM}^2$$

$$G_2=2C_C(C_A+C_B)$$

Then $B_4$ can be written as:

$$B_4=R_S\frac{C_C^2cos^2{\beta}+G_2cos{\beta}+G_1}{C_9+C_Ccos{\beta}}$$

$$B_4=\underbrace{\overbrace{\overbrace{\frac{R_S}{C_9+C_Ccos{\beta}}}^{\mathbf{\color{Green}{Term1}}}C_C^2cos^2{\beta}}^{\mathbf{\color{Blue}{Term2}}}+\underbrace{\overbrace{\frac{R_S}{C_9+C_Ccos{\beta}}G_2cos{\beta}}^{\mathbf{\color{Magenta}{T_1G_2cos{\beta}}}} +\overbrace{\frac{R_S}{C_9+C_Ccos{\beta}}G_1}^{\mathbf{\color{Cyan}{Term3}}}}_{\mathbf{\color{Bittersweet}{Sum2}}}}_{\mathbf{\color{Orange}{Sum3}}}$$

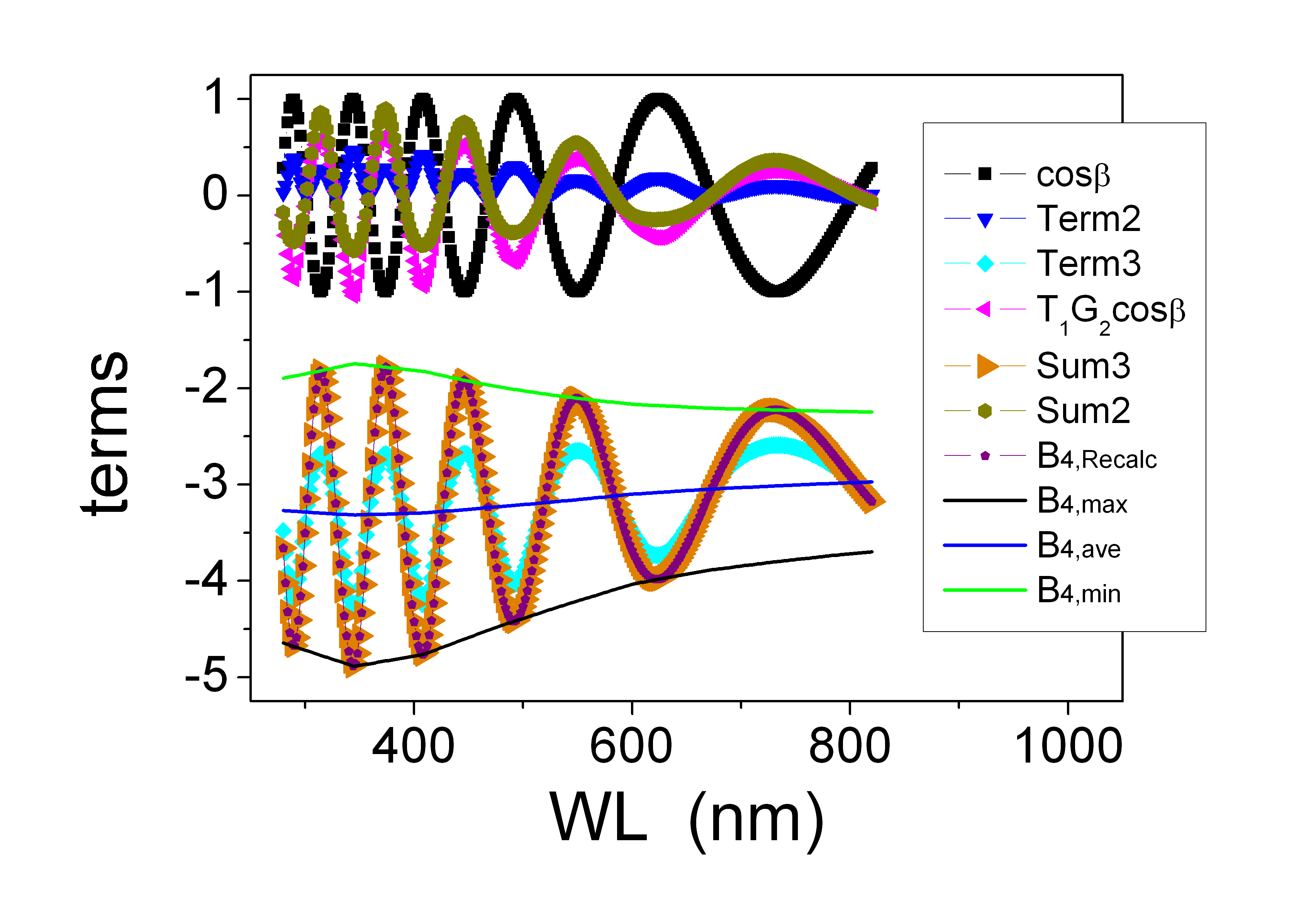
The term in $(cos\beta)^2$ oscillates with half the period $(cos\beta)$ terms. This does not affect the general period of oscillation, because the $(cos\beta)^2$ term is in phase in the minima and opposite in phase in the maxima of other oscillating terms. When summed up, this has the effect of inserting an offset in the average value; and in modifying the overall function in something different from a pure sinusoidal; but not much different, so that $B_4$ can still be approximated as a constant times an oscillating $(cos\beta)$ factor. 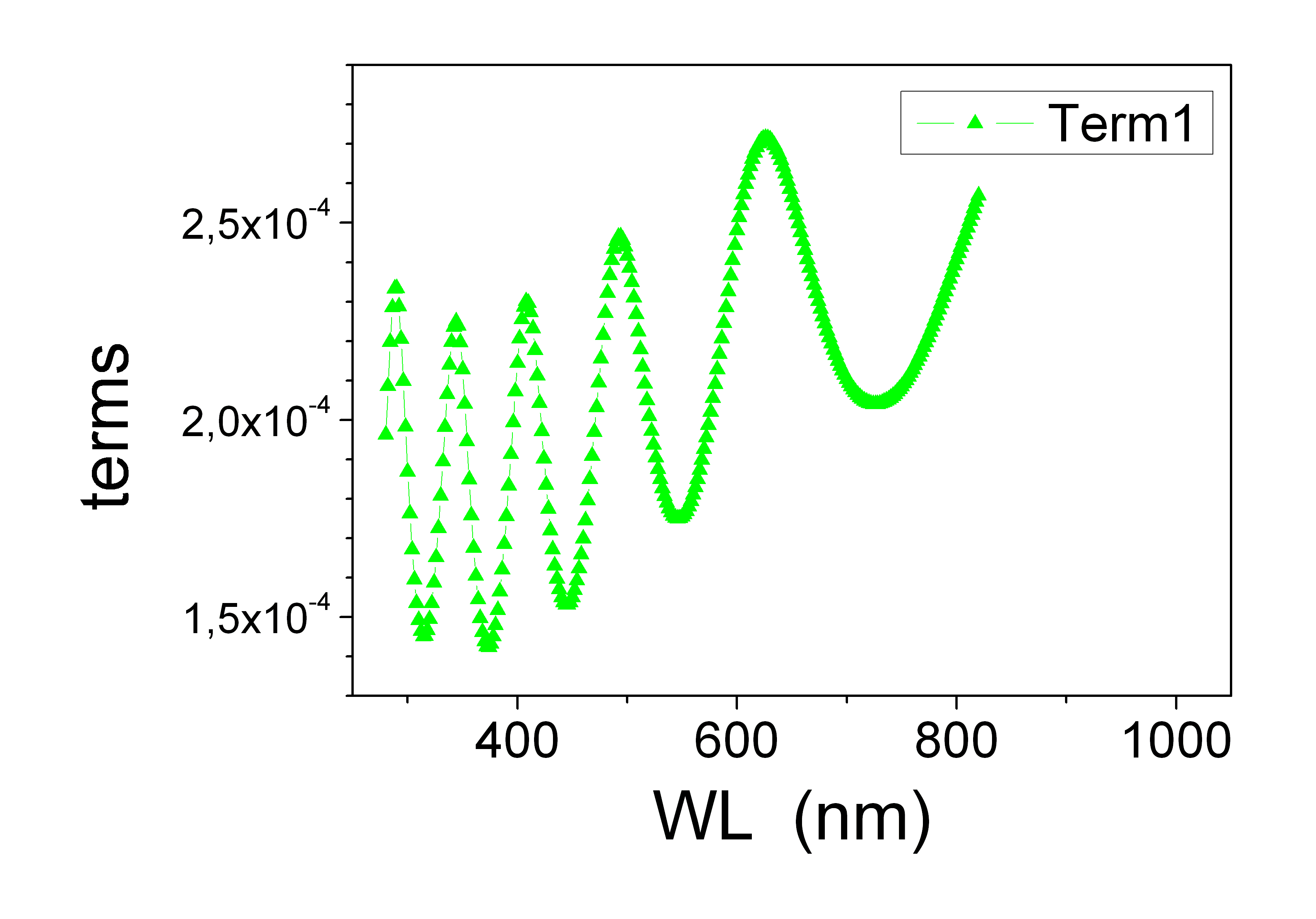Actually, only Term1 oscillates as $(cos\beta)$, although it contains $(cos\beta)$ at the denominator; its coefficient is negative, and this is why it does not oscillate as $-(cos\beta)$. However, the phase of Term1 has little effect on the final result, because it is multiplied by the term in $(cos\beta)^2$ that, as said above, it has half the period of $(cos\beta)$.
The term $\color{magenta}{T_1G_2cos\beta}$ has a negative coefficient, and oscillates as $-(cos\beta)$.
Term3 contains $(cos\beta)$ at the denominator, and oscillates as $-(cos\beta)$ because $G_1$ is negative.
The difference of the extrema $B_{4(-1)}$ and $B_{4(1)}$, as defined in the paper, is also negative. This is why the approximation of $B_4$ definition, with $(cos\beta)$ as oscillating factor, holds, see plot of terms Sum3 and $\color{purple}{B_{4,Recalc}}$ in the figure on the right.

$$A=\frac{B_{4,(1)}-B_{4,(-1)}}{2}$$
$$B_{4,(1)}=R_S\frac{(C_A+C_B)^2-T_{NUM}^2+2C_C(C_A+C_B)+C_C^2}{C_9+C_C}$$	*B_4,(1)*
$$B_{4,(-1)}=R_S\frac{(C_A+C_B)^2-T_{NUM}^2-2C_C(C_A+C_B)+C_C^2}{C_9-C_C}$$	*B_4,(-1)*
$$B_4\approx \;B_{4(average)}+Acos{\beta}$$	*B_4,Recalc*

Here, some comments are given on why the term $\mathbf{A(cos\beta)}$ cancels with $\mathbf{R_SC_C}$

$$A=\frac{B_{4,(1)}-B_{4,(-1)}}{2}$$

If we set:

$$Z=\left[(C_A+C_B)^2-T_{NUM}^2\right]+C_C^2 \hspace{30pt} Y=2C_C(C_A+C_B)$$ $$B_{plus}=R_S\left(\frac{Z}{C_9+C_C}+\frac{Y}{C_9+C_C}\right) \hspace{17pt} B_{minus}=R_S\left(\frac{Z}{C_9-C_C}-\frac{Y}{C_9-C_C}\right)$$ $$A=\frac{B_{plus}-B_{minus}}{2}$$ $$A=\frac{R_S}{2}\left(\frac{Z}{C_9+C_C}+\frac{Y}{C_9+C_C}-\frac{Z}{C_9-C_C}+\frac{Y}{C_9-C_C}\right)$$ $$A=\frac{R_S}{2}\frac{Z(C_9-C_C)+Y(C_9-C_C)-Z(C_9+C_C)+Y(C_9+C_C)}{C_9^2-C_C^2}$$ $$A=R_S\frac{YC_9-ZC_C}{C_9^2-C_C^2}$$ $$A=\frac{R_SC_C}{C_9^2-C_C^2}\left(Y\frac{C_9}{C_C}-Z\right)$$ $$A=\left.R_SC_C\frac{\overbrace{2C_9(C_A+C_B)-(C_A+C_B)^2+T_{NUM}^2-C_C^2}^{\color{Blue}{\mathbf{Num}}}}{\underbrace{(C_9^2-C_C^2)}_{\color{Magenta}{\mathbf{Den}}}}\right\}\color{Cyan}{\mathbf{TermCirca1}}$$

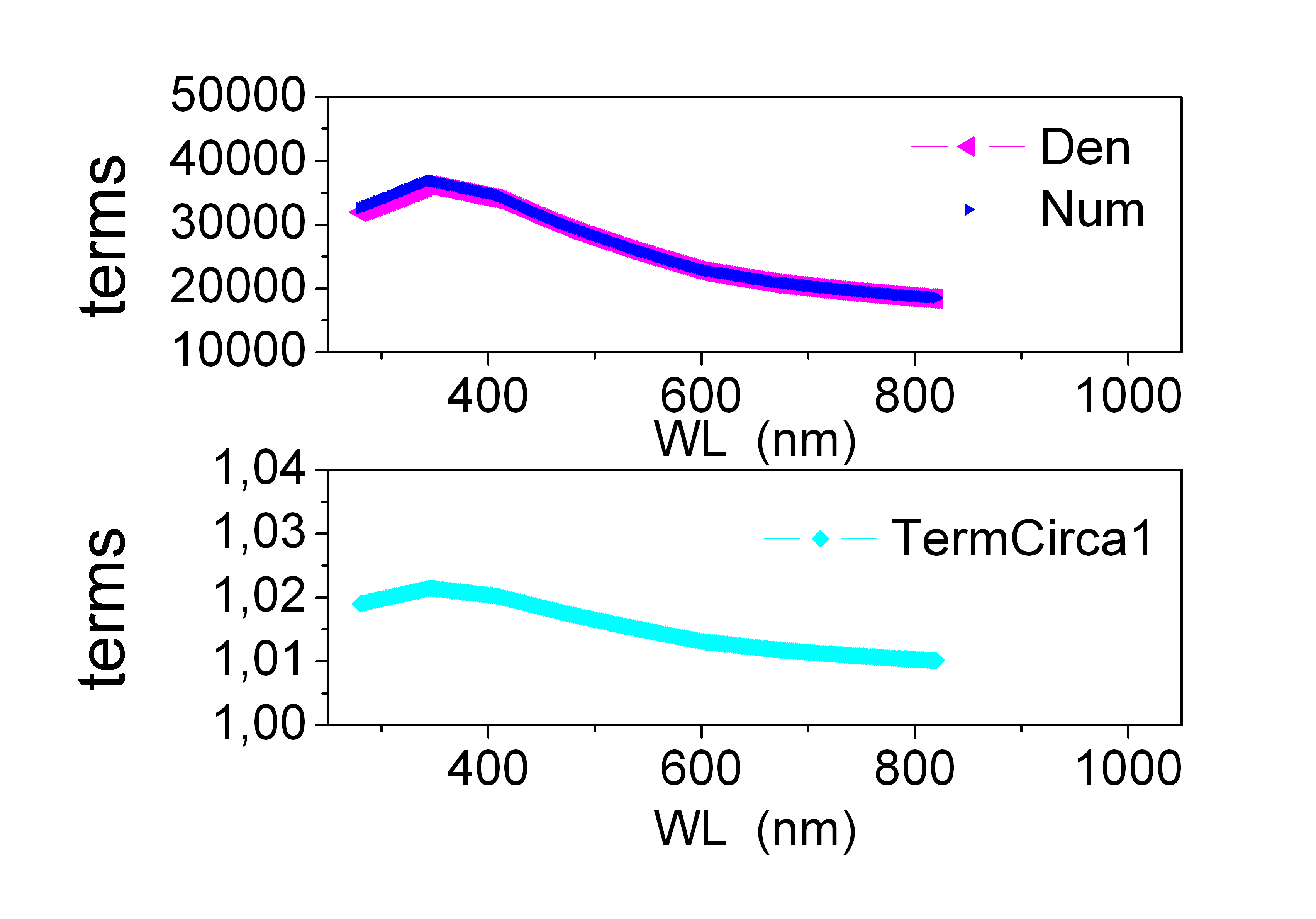
In this formula, numerator and denominator of the fraction are numbers of the order of 30000, but their ratio is equal to 1 within 2% at most. Therefore, A is approximately equal to R_sC_c, that justifies why the two terms cancel out. It remains to clarify why that ratio is so close to 1.

$$B_{4(average)}=\frac{B_{plus}+B_{minus}}{2}$$

Here, a rearrangement for $B_{4(Average)}$ is given, that can be replaced in the original formula.

$$B_{4(average)}=R_S\frac{ZC_9-YC_C}{C_9^2-C_C^2}$$

CNR-IMM, Laboratory of Optics

Some details on term $\mathbf{B_4}$

Back

Here, some comments are given on why the term $\mathbf{A(cos\beta)}$ cancels with $\mathbf{R_SC_C}$